Hello tuần mới anh em Mì AI, như vậy trong bài trước mình đã cùng nhau khởi động series về oánh giá model AI với hai khái niệm Loss và Accuracy tại đây. Hôm nay chúng ta sẽ đi tiếp series này với việc tìm hiểu các khái niệm Precision, Recall va F Score nhé.

Trong các bài toán thực tế, nhiều khi các yếu tố Loss và Accuracy chưa thể nói hết việc một model có “tốt” hay không? Tại sao lại thế? Để hiểu vấn đề ta có thể đi sâu vào một ví dụ như sau:

Giả sử như các bạn đang xây dựng model nhận diện ung thư cho người bệnh chẳng hạn.

• Model A các bạn đạt 99% accuracy đi. Quá tuyệt còn gì nữa? Không đâu, hãy tưởng tượng model của bạn đã để lọt một trường hợp bị ung thư thật nhưng model bạn dự đoán là không ung thư và người bệnh không điều trị dẫn đến …điều xấu nhất. Vậy bạn nghĩ sao? Model A của bạn có còn tuyệt nữa không?
• Model B chỉ đạt 96% thôi. Nhưng sau khi evaluate thì không có trường hợp nào bị ung thư bị bỏ sót. Model chỉ đạt 96% do có vài trường hợp không bị ung thư và bị chỉ định nhầm thành có ung thư (nhưng sau khi xét nghiệm kỹ lại thì đã khẳng định không bị ung thư và xuất viện rồi). Và giờ thì có khi Model B với acc thấp hơn lại ngon lành hơn đấy nhỉ 😀

Ok, ví dụ đơn giản vậy để các bạn biết rằng Accuracy quan trọng nhưng không phải là tất cả nhé. Và đó là lý do chúng ta đi tìm hiểu các khái nhiệm trong bài hôm nay.

Let’s go!

Khái niệm về Confusion Matrix

Nếu dịch tên của nó ra tiếng Việt thì sẽ là “Ma trận lú lẫn” =)). Nói thật là lúc đầu mình cũng đến lú lẫn và phải gọi là siêu confuse với nó. Nên mình sẽ cố gắng việt bài này thật đơn giản để các bạn có thể hiểu được.

Quay lại bài toán chẩn đoán ung thư (output trả về có/không ung thư). Sau khi xây dựng xong model và chạy predict với toàn bộ dữ liệu thì ta kẻ cái bảng như sau:

Đó, thế thôi, cái bảng “Con phu sần mắc trích” chính là cái trên đó. Tóm lại là nó tổng kết giữa nhãn thực tế của dữ liệu với nhãn do model dự đoán ra thôi. Ví dụ như bảng trên, ta có thể phân tích như sau:

• Đầu tiên nhìn dòng số 1 nào. Như vậy thực tế trong dữ liệu có 990 người ung thư và đều được model nhận đúng là Ung thư, không có ai bị dự đoán nhầm thành Không ung thư quá. Khá tốt.
• Bây giờ nhìn dòng số 2, tổng dữ liệu của chúng ta có 5+5 = 10 người Không bị ung thư. Trong đó 5 người đã bị nhận nhầm thành Ung thư và 5 người đã được nhận đúng là Không ung thư.

Có thế thôi mà! Đơn giản đúng không các bạn. Bây giờ chúng ta sẽ thay đổi cách nhìn một chút để cho trông nó khoa học hơn và có vẻ “nguy hiểm”hơn như sau.

Trong bài toán trên, output của bài toán có 2 class : Ung thư và Không ung thư. Bây giờ ta chọn 1 lớp nguy hiểm hơn (đó là Ung thư) làm lớp Positive và lớp còn lại là Negative và tiến hành thay nhãn:

Từ đó ta có các khái niệm: True Positive , False Negative , False Positive và True Negative. Với bài toán trên thì:

• TP = 990
• FN = 0
• FP =TN = 5

Đấy, cái bảng Confusion Matrix nó chỉ có thế thôi. Bây giờ ta đi tìm hiểu các món bên dưới xem nó là cái gì nào.

Khái niệm về Precision

Nói về món này thì ta cứ xét cái công thức cái nào:

$$\large Precision = \frac{True Positive}{True Positive+False Positive}$$

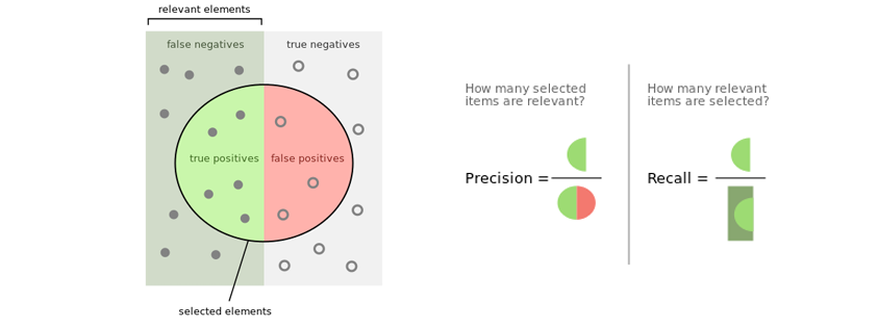
Như vậy, có thể thấy Precision chả là cái quái gì ngoài tỷ lệ giữa số sample được tính là True Positive (TP) với tổng số sample được phân loại là Positive (bằng chính TP + FP). Chú ý đường màu đỏ bên trên hình trên.

Và khi đó 0< Precision <=1, Precision càng lớn có nghĩa là độ chính xác của các điểm tìm được càng cao. Ví dụ như bài trên trong 995 điểm được nhận là Positive thì có 990 điểm là TP và 5 điểm là FP nên ta có Precision khá cao:

$$\large Precision = \frac{990}{990+5} = 0.995$$

Precision sẽ cần được coi trọng hơn khi lựa chọn model với các bài toán cụ thể khi mà việc nhận nhầm False Positive mang lại kêt quả tồi tệ. Ví dụ với bài toán chặn Spam Mail chẳng hạn, khi đó việc nhận nhầm FP (nhầm 1 mail thường thành mail spam) sẽ làm ảnh hưởng đến công việc của người dùng vì miss một cái mail quan trọng (hợp đồng hàng nghìn tỷ đồng chẳng hạn).

Khái niệm về Recall

Thế còn Recall là gì? Cũng same same, ta có công thức của Recall:

$$\large Recall = \frac{True Positive}{True Positive+False Negative}$$

Công thức trên có nghĩa là tỷ lệ giữa các điểm positive thực được nhận đúng trên tổng điểm positive thực. Như vậy, Recall cao có nghĩa tỉ lệ bỏ sót các sample positive thực thấp. Chú ý đường màu xanh bên trên hình trên.

Do đó, Recall nên được gán trọng số cao hơn khi cân nhắc lựa chọn model tốt nhất khi mà việc nhận nhầm các nhãn Positive thực thành False Negative mang lại hậu quả khôn lường. Ví dụ như bài toán ung thư bên trên kìa, việc nhận nhầm người Ung thư thành người bình thường và trả về nhà không điều trị sớm thì….thôi mình không muốn nói thêm nữa.

Cụ thể khi áp dụng công thức thì với bài ung thư bên trên ta có

$$\large Recall = \frac{990}{990+0} = 1$$

Amazing! Model của chúng ta không bỏ sót một sample positive thực nào! Wow!

Khái niệm về F-1 Score

Như vậy chúng ta đã có 2 khái niệm Precision và Recall và mong muốn 2 thằng này càng cao càng tốt. Tuy nhiên trong thực tế nếu ta điều chỉnh model để tăng Recall quá mức có thể dẫn đến Precision giảm và ngược lại, cố điều chỉnh model để tăng Precision có thể làm giảm Recall. Nhiệm vụ của chúng ta là phải cân bằng 2 đại lượng này.

Vậy thì bài toán mới được đặt ra là: giả sử chúng ta đang xây dựng một tập các model (để sau đó chọn ra model tốt nhất). Và chúng ta như “đứng giữa 2 con đường” khi lựa chọn các model sao cho cân bằng giữa Precision và Recall. Nhưng thật may có thêm một tham số nữa dung hòa giữa 2 cái và ta có thể căn vào đó để lựa chọn, đó là F-1 Score:

$$\large F1 = 2\frac{Precision*Recall}{Precision+Recall}$$

Đó, giờ anh em cứ căn vào F1 mà chọn model, F1 càng cao thì càng tốt. Khi lý tưởng nhất thì F1 = 1 (khi Recall = Precision=1).

Quay lại ví dụ bài toán ung thư, ta lại có:

$$\large F1 = 2\frac{0.995*1}{0.995+1} = 0.997$$

ROC Curve

Chúng ta sẽ tìm hiểu món Receiver Operating Characteristic (ROC) curve. Nghe cái tên thôi đã thấy hoành tráng rồi, kaka.

Để vẽ ROC ta sẽ sử dụng thêm 2 khái niệm nữa:

• Đầu tiên là True Positive Rate (TPR) chính là Recall
• False Positive Rate (FPR) là tỷ lệ cảnh báo sai.

$$\large True Positive Rate = \frac{True Positive}{True Positive+False Negative}$$

$$\large False Positive Rate = \frac{False Positive}{False Positive+True Negative}$$

Thực chất cái đường ROC để chúng ta show lên mối quan hệ giữa TPR và FPR khi chúng ta thay đổi ngưỡng threshold của model. Ví dụ ta có thể đặt một ngưỡng threshold=0.5 khi phân loại mail rác chẳng hạn, các mail nào có probability trên threshold sẽ được coi là mail rác. Bây giờ chúng ta sẽ thay đổi threshold để xem sự thay đổi của TPR và FPR trên đồ thị.

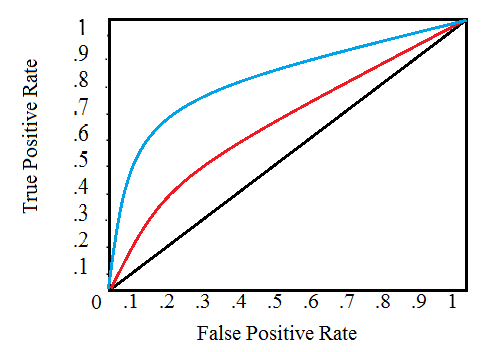
Sau khi tính toán các đại lượng, chúng ta sẽ vẽ độ thị biểu diễn chúng ứng với sự thay đổi threshold như hình trên.

Khi threshold = 1.0, chúng ta sẽ ở góc dưới trái bỏi vì model của chúng ta không predict bất kì điểm nào là positive và dẫn tới true positives = false positives = 0 (hay TPR = FPR = 0). Khi ta giảm dần threshold, số sample được predict là positivte tăng lên và dẫn tới true positive và false positive cũng tăng. Khi threshold về 0 thì TPR = FPR = 1 và chúng ta lên đỉnh trên cùng bên phải.

Việc vẽ đồ thị ROC sẽ dẫn tới một khái niệm tính toán vùng nằm dưới đường ROC (Area Under the Curve – AUC ). Đại lượng này có giá trị từ 0-1, giá trị càng cao thì model càng tốt và có nghĩa là đường ROC càng cong sát phía trên. Ví dụ như hình trên, đường màu xanh có AUC lớn hơn thể hiện model tốt hơn.

Trong bài sau mình sẽ cùng nhau thực hành các món tính toán này và các bạn sẽ hiểu rõ hơn nhé.

Tổng kết vấn đề

Well! Như vậy các bạn thấy đó, chúng ta đã có một vài thứ mới trong bài này như sau:

True positives: Các điểm Positive thực được nhận Đúng là Positive

False positives: Các điểm Negative thực được nhận Sai là Positive

True negatives: Các điểm Negative thực được nhận Đúng là Negative

False negatives: Các điểm Positive thực được nhận Sai là Negative

Recall:  Thể hiện khả năng phát hiện tất cả các postivie, tỷ lệ này càng cao thì cho thấy khả năng bỏ sót các điểm Positive là thấp

Precision: Thể hiện sự chuẩn xác của việc phát hiện các điểm Positive. Số này càng cao thì model nhận các điểm Positive càng chuẩn.

F1 score: Là số dung hòa Recall và Precision giúp ta có căn cứ để lựa chọn model. F1 càng cao càng tốt ;).

Đường ROC : Thể hiện sự tương quan giữa Precision và Recall khi thay đổi threshold.

Area Under the ROC: Là vùng nằm dưới ROC, vùng này càng lớn thì model càng tốt.

Như vậy có bạn sẽ hỏi nếu có nhiều hơn 2 class thì tính các món trên như thế nào? Khi đó bạn có thể xây dựng bảng Confusion Matrix cho mỗi lớp bằng cách ta coi lớp đó là lớp Positive, còn tất cả các lớp còn lại ta gộp chung vào thành một lớp Negative là done!

Đó, đại khái như vậy, bài này đã quá dài rồi nên mình xin tạm dừng. Trong bài sau chúng ta sẽ cùng thực hành tính toán, show ra các thông số này bằng Python để các bạn hiểu rõ hơn nhé. Hẹn gặp lại các bạn!

Hãy join cùng cộng đồng Mì AI nhé!

Fanpage: http://facebook.com/miaiblog
Group trao đổi, chia sẻ: https://www.facebook.com/groups/miaigroup
Website: https://miai.vn
Youtube: http://bit.ly/miaiyoutube